Calculates the height of a radar beam as a function of elevation and range, assuming the beam is emitted at surface level.
beam_height(range, elev, k = 4/3, lat = 35, re = 6378, rp = 6357)Arguments
- range
Numeric. Slant range, i.e. the length of the skywave path between target and the radar antenna, in m.
- elev
Numeric. Beam elevation, in degrees.
- k
Numeric. Standard refraction coefficient.
- lat
Numeric. Geodetic latitude of the radar, in degrees.
- re
Numeric. Earth equatorial radius, in km.
- rp
Numeric. Earth polar radius, in km.
Value
numeric. Beam height in m.
Details
To account for refraction of the beam towards the earth's surface, an
effective earth's radius of k * (true radius) is assumed, with k = 4/3.
The earth's radius is approximated as a point on a spheroid surface, with
re the longer equatorial radius, and rp the shorter polar
radius. Typically uncertainties in refraction coefficient are relatively
large, making oblateness of the earth and the dependence of earth radius with
latitude only a small correction. Using default values assumes an average
earth's radius of 6371 km.
See also
Other beam_functions:
beam_distance(),
beam_profile(),
beam_profile_overlap(),
beam_range(),
beam_width(),
gaussian_beam_profile()
Examples
# Beam height in meters at 10 km range for a 1 degree elevation beam:
beam_height(10000, 1)
#> [1] 180.4081
# Beam height in meters at 10 km range for a 3 and 5 degree elevation beam:
beam_height(10000, c(3, 5))
#> [1] 529.229 877.398
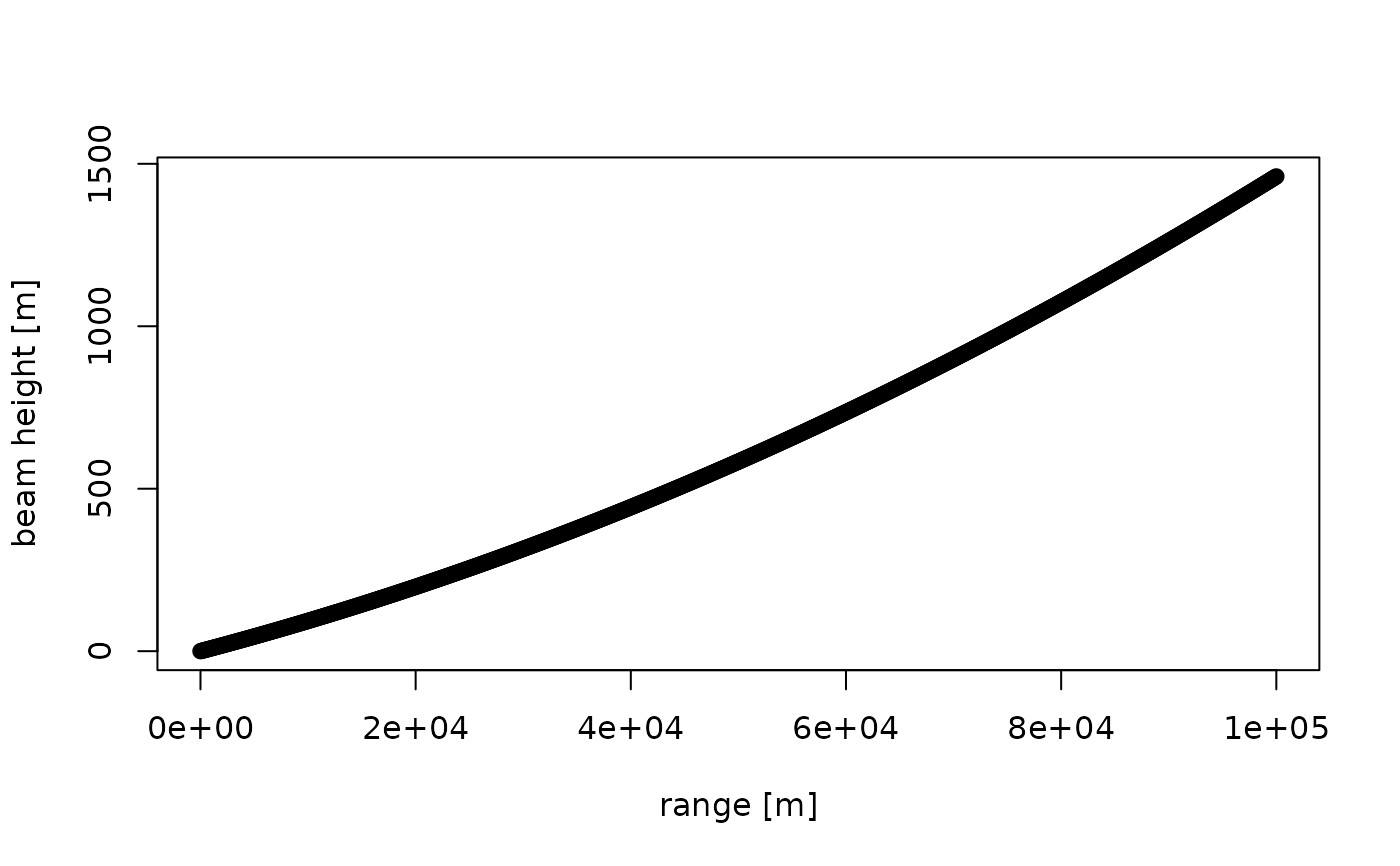
# Define ranges from 0 to 1000000 m (100 km), in steps of 100 m:
range <- seq(0, 100000, 100)
# Plot the beam height of the 0.5 degree elevation beam:
plot(range, beam_height(range, 0.5), ylab = "beam height [m]", xlab = "range [m]")
